LDPC编译码原理
 发布时间:2021-07-01
阅读量:50
分享:
发布时间:2021-07-01
阅读量:50
分享:
https://blog.csdn.net/sinat_38151275/article/details/98102699
LDPC码简介
低密度校验码(LDPC码)是一种前向纠错码,LDPC码最早在20世纪60年代由Gallager在他的博士论文中提出,但限于当时的技术条件,缺乏可行的译码算法,此后的35年间基本上被人们忽略,其间由Tanner在1981年推广了LDPC码并给出了LDPC码的图表示,即后来所称的Tanner图。1993年Berrou等人发现了Turbo码,在此基础上,1995年前后MacKay和Neal等人对LDPC码重新进行了研究,提出了可行的译码算法,从而进一步发现了LDPC码所具有的良好性能,迅速引起强烈反响和极大关注。经过十几年来的研究和发展,研究人员在各方面都取得了突破性的进展,LDPC码的相关技术也日趋成熟,甚至已经开始有了商业化的应用成果,并进入了无线通信等相关领域的标准。
LDPC码的特点
LDPC码是一种分组码,其校验矩阵只含有很少量非零元素。正是校验矩阵的这种稀疏性,保证了译码复杂度和最小码距都只随码长呈现线性增加。除了校验矩阵是稀疏矩阵外,码本身与任何其它的分组码并无二致。其实如果现有的分组码可以被稀疏矩阵所表达,那么用于码的迭代译码算法也可以成功的移植到它身上。然而,一般来说,为现有的分组码找到一个稀疏矩阵并不实际。不同的是,码的设计是以构造一个校验矩阵开始的,然后才通过它确定一个生成矩阵进行后续编码。而LDPC的编码就是本文所要讨论的主体内容。对于LDPC码而言,校验矩阵的选取十分关键,不仅影响LDPC码的纠错性能力,也影响LDPC编译码的复杂度及硬件实现的复杂度。准循环 LDPC 码(Quasi-Cycle,QC-LDPC)是 LDPC 码中重要的一类,是指一个码字以右移或左移固定位数的符号位得到的仍是一个码字。QC-LDPC 码的校验矩阵是由循环子矩阵的阵列组成,相对于其他类型的 LDPC 码,在编码和解码的硬件实现上具有许多优点。编码可以通过反馈移位寄存器有效实现,采用串行算法,编码的复杂度与校验比特位数成正比,而采用并行算法,编码复杂度与码字长度成正比。对硬件解码实现,准循环的结构简化了消息传递的路径,可以部分并行解码,实现了解码复杂度和速率的折中。这些优点,使得 QC-LDPC 码作为未来通信和存储系统应用的主要 LDPC 码。
译码算法的选择
译码方法是LDPC码与经典的分组码之间的最大区别。经典的分组码一般是用ML类的译码算法进行译码的,所以它们一般码长较小,并通过代数设计以减低译码工作的复杂度。但是LDPC码码长较长,并通过其校验矩阵H的图像表达而进行迭代译码,所以它的设计以校验矩阵的特性为核心考虑之一。由于 LDPC 码校验矩阵的稀疏性,其译码复杂度与码长不是指数关系,而是线性关系,因而 LDPC 码的码长可以很长,可以达到几千到几万甚至更高,这样带来的一个好处是:一个码字内各比特之间的关联长度比较长,一般通过迭代译码方法进行译码,充分利用码字内各比特的关联性以提高译码准确度,并且还充分利用了信道的特征。本课题采用的译码算法为置信传播(BP)译码算法,置信传播算法是基于 Tanner 图的迭代译码算法。在迭代过程中,可靠性信息,即“消息”通过 Tanner图上的边在变量节点和校验节点中来回传递,经多次迭代后趋于稳定值,然后据此进行最佳判决,BP译码算法有着非常好译码性能。
Tanner图
LDPC码常常通过图来表示,而Tanner图所表示的其实是LDPC码的校验矩阵。Tanner图包含两类顶点:n个码字比特顶点(称为比特节点),分别与校验矩阵的各列相对应和m个校验方程顶点(称为校验节点),分别与校验矩阵的各行对应。校验矩阵的每行代表一个校验方程,每列代表一个码字比特。所以,如果一个码字比特包含在相应的校验方程中,那么就用一条连线将所涉及的比特节点和校验节点连起来,所以Tanner图中的连线数与校验矩阵中的1的个数相同。以下图是矩阵的Tanner图,其中比特节点用圆形节点表示,校验节点用方形节点表示,加黑线显示的是一个6循环:

Tanner图中的循环是由图中的一群相互连接在一起的顶点所组成的,循环以这群顶点中的一个同时作为起点和终点,且只经过每个顶点一次。循环的长度定义为它所包含的连线的数量,而图形的围长,也可叫做图形的尺寸,定义为图中最小的循环长度。如上图中,图形的尺寸,即围长为6,如加黑线所示。

LDPC编码
基于校验矩阵H直接编码方案
首先推导出根据校验矩阵直接编码的等式。将尺寸为(m,n)校验矩阵写成如下形式:

其中H1的大小为m ∗ k ,H2 的大小为m ∗ m 。设编码后的码字行向量为c,它的长度为n,把它写成如下形式

其中s是信息码的行向量,长度为k,p为检验行向量,长度为m,根据校验公式

上式展开得

展开该矩阵方程,并考虑到运算是在GF(2)中进行的,得到

如果校验矩阵H是非奇异的,则满秩,所以有

这样就把码字的校验位计算出来了,这种方法需要保证H2 是可逆的,而准循环LDPC码因其结构化的特点可以保证这一条件。
基于生成矩阵G的编码方案
令LDPC码的校验矩阵H分为两部分:

其中子矩阵P的大小为c×c,Q的大小为c×m。计算

其中的矩阵运算为模二运算。求得的m×c矩阵W必定是一个稠密的准循环结构矩阵。由稠密的准循环结构矩阵W可以求得生成矩阵:

其中I是m×m的单位矩阵。可以看出生成矩阵具有准循环结构特性。得到生成矩阵G后将码字X与其相乘C=X*G,获得编码后的码字C。这里的乘法要满足有限域的乘法法则。
LDPC译码
Gallager 在描述 LDPC 码的时候,分别提出了硬判决译码算法和软判决译码算法两种。经过不断发展,如今的硬判决算法已在 Gallager 算法基础上进展很多,包含许多种加权比特翻转译码算法及其改进形式。硬判决和软判决各有优劣,可以适用于不同的应用场合。
比特翻转算法(BF)
硬判决译码算法最早是 Gallager 在提出 LDPC 码软判决算法时的一种补充。硬判决译码的基本假设是当校验方程不成立时,说明此时必定有比特位发生了错误,而所有可能发生错误的比特中不满足校验方程个数最多的比特发生错误的概率最大。在每次迭代时均翻转发生错误概率最大的比特并用更新之后的码字重新进行译码。具体步骤如下:
设置初始迭代次数 k1及其上限kmax 。对获得的码字y=(y1,y2…yn)按照下式展开二元硬判决得到接收码字的硬判决序列Zn 。

若k1=kmax ,则译码结束。不然,计算伴随式s=(s0,s1,…sm-1),sm表示第m个校验方程的值。若伴随式的值均为 0,说明码字正确,译码成功。否则说明有比特位错误。继续进行步骤3。
对每个比特,统计其不符合校验方程的数量fn (1<=n<=N)

4. 将最大fn 所对应的比特进行翻转,然后k=k+1,返回步骤2。
BF 算法的理论假设是若某个比特不满足校验方程的个数最多,则此比特是最有可能出错的比特,因此,选择这个比特进行翻转。BF 算法舍弃了每个比特位的可靠度信息,单纯的对码字进行硬判决,理论最为简单,实现起来最容易,但是性能也最差。当连续两次迭代翻转函数判断同一个比特位为最易出错的比特时,BF 算法会陷入死循环,大大降低了译码性能。
置信传播算法(BP)
置信传播(Belief Propagation)译码算法是消息传递(Message Passing)算法在 LDPC译码中的运用。消息传递算法是一个算法类,最初运用于人工智能领域,人们将其运用到 LDPC 码的译码算法中,提出了LDPC 码的置信传播算法。置信传播算法是基于 Tanner 图的迭代译码算法。在迭代过程中,可靠性信息,即“消息”通过 Tanner图上的边在变量节点和校验节点中来回传递,经多次迭代后趋于稳定值,然后据此进行最佳判决。
在介绍BP译码算法之前需要先了解一下Tanner图的概念。
Tanner图是一种表示LDPC码的双向图,图的下面每个节点表示码字的一个比特位,称比特节点(bit nodes)。上面每个节点称为校验节点(check nodes)。校验矩阵中为1的元素,表示Tanner图中比特节点和校验节点之间存在连接边,这条边可称为两端节点的相邻边,相邻边两端的节点称为相邻节点,每个节点相邻边数称为该节点的度数。Tanner图是用来描述LDPC码结构的有效工具,同时也是迭代译码算法的参考工具。在Tanner图中校验节点和变量节点之间可以进行消息的可靠传递,首先变量节点接收初始化后验概率进行计算,将得到的可靠信息传递给相邻的校验节点;经过校验节点更新算法的计算,再将得到的运算结果传回至与其相邻的变量节点处,随后变量节点再将由校验节点得到的可靠信息以及初始化后验概率信息进行处理;将最后得到的有效信息进行判决得到译码结果。
LDPC码的译码较为复杂,下面以置信传播算法举一个简单的例子来说明一下。
发送码字C=(C9,C8,C7,C6,C5,C4,C3,C2,C1),其监督矩阵H是

则C必然满足线性方程组HCT = 0 ,即

通过信道后接收到的码字Y=(Y0,Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8,Y9)可能包含错误,因此伴随式S= HYT ≠ 0 。将此线性方程组用如图所示的Tanner图来表示。
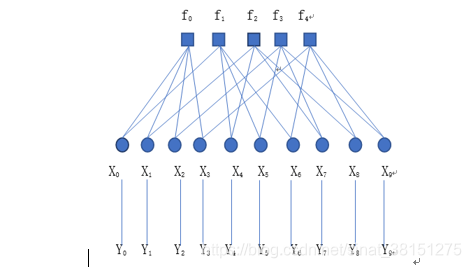
图中的X0,X1…X9称为变量节点,代表10个比特C0,C1,C2…C9,它们是译码器待求解的未知变量。图中的□成为校验节点,代表线性方程组中的每一个校验方程,连线就代表方程中此变量的系数为1。
译码过程是在变量节点和校验节点之间传递信息。每个变量节点告诉它所连接的校验节点“我认为该变量是什么”,而校验节点告诉它所连接的变量节点“我认为该变量应该是什么”。经过反复的消息传递后,变量节点和校验节点不断改变自己对各个变量是什么的看法,最终能形成一个满足校验方程的码字,这就是译码的结果。如果经过充分的迭代后仍然不能形成一个满足校验方程的码字,则译码器宣布它无法译出这个码字,即译码失败。
置信传播译码算法的基本流程如下:
在迭代前,译码器接收到信道传送过来的实值序列y=(y1,y2,….yn),所有变量节点bi接收到对应的接收值yi。
第一次迭代:每个变量节点给所有与之相邻的校验节点传送一个可靠性消息,这个可靠性消息就是信道传送过来的值;每个校验节点接收到变量节点传送过来的可靠性消息之后,进行处理,然后返回一个新的可靠性信息给与之相邻的变量节点,这样就完成了第一次迭代;此时可以进行判决,如果满足校验方程,则不需要再迭代,直接输出判决结果,否则进行第二次迭代。
第二次迭代:每个变量节点处理第一次迭代完成时校验节点传送过来的可靠性消息,处理完成后新的消息发送给校验节点,同理,校验节点处理完后返回给变量节点,这样就完成了第二次迭代。完成后同样进行判决,如果满足校验方程则结束译码,否则如此反复多次迭代,每次都进行判决,直到达到设定的最大迭代次数,译码失败。在每次迭代过程中,无论是变量节点传送给校验节点的信息或者校验节点传送给变量节点的信息,都不应该包括前次迭代中接收方发送给发送方的信息,这样是为了保证发送的信息与接收节点已得到的信息相互对立。
假设在 AWGN 信道中,信道编码后的码字C=(c1,c2,…,cn)通过调制映射为调制序列X=(x1,x2…,xn),然后经信道传输,接收的序列为y=(y1,y2…,yn)。
为后面章节的推导方便,先介绍一引理。
引理:
一个独立的比特序列,其长度为m,假设第i个比特为 1 的概率为pi ,则整个序列中出现偶数个1的概率为

出现奇数个 1 的概率为

这是信道编码领域中经常使用的一个定理,故直接使用。
Gallager 定理:对于(n,j,k)规则 LDPC 码,Pil 第i个校验方程中第 l 校特为1的概率,则

其中:
Pr (xi =0∣{y},S)表示在程组为S ,接收序列为y的条件下判断发送帧中的第i个比特为0的概率
Pr(xi =1∣{y},S)表示在程组为S,接收序列为 y的条件下判断发送帧中的第i个比特为0的概率
pi 表示发送序列的第 i位为1的先验概率;
M(i) 表示校验节点的集合,集合中的节点均与变量节点i相邻;
N(j) 表示变量节点的集合,集合中的节点均与校验节点 j相邻。
由上节介绍的 BP 算法的原理及 Gallager 定理中的描述可知,变量节点i传递给校验节点j的可靠性信息q{ij}(1)就是Pr(Xj=1|{y},S),于是定义

表示变量节点i ii传递给校验节点j 的外部概率信息,即在得到除校验节点j以外的其他所有校验比特和信道的外部信息后,判断变量节点ci =1的概率。
再定义

表示变量节点i传递给校验节点 j 的外部概率信息,即在得到除j 以外的其他所有校验比特和信道的外部信息后,判断变量节点ci =0的概率。
另一方面,校验节点 j传递给变量节点i的可靠性信息应该为在给定信息位和其他信息位具有独立概率分布条件下,校验方程 j满足的概率。将此可靠性信息记为rji ,则

将上式代入

根据以上的描述和符号定义,概率 BP 译码算法流程可以归纳为如下几个步骤:
(1) 初始化
计算经信道传输后各变量节点的初始概率pi(1)和pi (0)。然后对每个变量节点求传递给与其相邻的校验节点的可靠性信息

其中的上标(0)表示迭代次数。
2) 校验节点处理过程(rij 的计算)
求出第l ll次迭代过程中校验节点i递给与之相邻的变量节点j可靠性信息

其中的上标(l)和(l−1)均表示迭代次数。
(3)变量节点处理过程(qij 的计算)
求出第l 次迭代过程中变量节点j传递给与之相邻的校验节点i ii的可靠性信息

其中的Kij 是校正因子,使每次计算出的
(4)译码判决
在本次迭代过程处理最后,重新计算各变量节点的可靠性信息

其中的 Kj 也为校正因子,目的是使
如果 ,那么这一点的估计值时ci=1,否则估计值为ci= 0。如果估计值满足奇偶校验方程,那么终止算法,否则算法继续运行,直到达到预先设置的最大迭代次数。
,那么这一点的估计值时ci=1,否则估计值为ci= 0。如果估计值满足奇偶校验方程,那么终止算法,否则算法继续运行,直到达到预先设置的最大迭代次数。
仿真验证
| LDPC码 | 基于IEEE 802.16e标准 |
| 码长 | 1440 |
| 码率 | 1/2 |
| 有限域 | 四元 |
| 迭代次数 | 20 |
| 调制方式 | QPSK |
| 单一信噪比下仿真次数 | 10^5 |
| 最小误码总数 | 不少于200 |
| 信道 | 高斯信道 |
仿真说明如下:
下图是在高斯信道下,码字经过LDPC编码和未编码的译码结果对比图,为了保证对比的有效性,仿真中LDPC码与未编码的码字等长,同为1440,LDPC码通过BP译码算法译码,而未编码的码字通过解调硬判决译码。
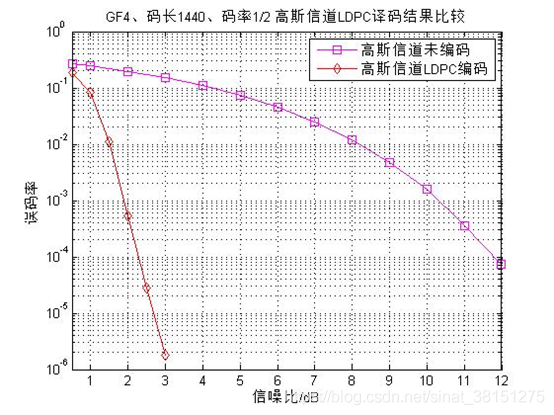
仿真结果分析:从图可以看出码字经过LDPC编译码之后其抵抗噪声的能力极大加强,与未编码的码字相比,在误码率都为1e-4时,其性能提高了9.5dB左右,从而验证了LDPC码是一种性能极佳的信道纠错码。
结束语
目前LDPC码研究领域的主要工作集中在译码算法的性能分析、编码方法、码的优化算法等,经过研究人员的努力,LDPC码的研究取得很大进展,但仍有许多问题需要进一步研究:
(1)LDPC码校验矩阵的构造,尽管在构造最优的LDPC码方面取得了一些进步,但目前还没有一套系统的办法来构造所需要的好码,特别是在码字长度有限、码率一定的条件下,构造性能优异的好码是一个非常具有挑战性的课题。
(2)LDPC编码系统的联合优化设计,将编码技术与调制技术、均衡技术、时空编码技术、OFDM技术结合进行性能优化是当前及将来的发展方向之一。
(3)无线衰落信道及MIMO技术下LDPC码的性能分析方法及优化设计准则。目前LDPC码字的优化设计主要在加性高斯白噪声信道下得到的,而无线衰落信道下,特别是时变信道非线性环境下码字的性能分析方法、优化设计准则和信道估计的影响也是非常关键的课题,需要进一步的研究探索。
此外,基于LDPC码的链路自适应技术,LDPC码在集成通信网物理层、应用层联合优化系统中的应用,LDPC码在无线局域网和深空宇航中的应用,基于LDPC码的图像传输、图像数字水印系统中的应用以及寻找更适合硬件实现的LDPC码编译码方法等都是非常值得研究的课题。
服务中心
最新方案

地面站控管理系统
其他学院知识



 6163银河net163am学院 >
6163银河net163am学院 > 深圳市南山区西丽街道打石一路深圳国际创新谷7栋B座8楼
深圳市南山区西丽街道打石一路深圳国际创新谷7栋B座8楼 +86-755-82513818
+86-755-82513818 +86-755-82513868
+86-755-82513868
